Chuyên đề: Khúc xạ ánh sáng và lưỡng chất phẳng

Dạng 1: Áp dụng định luật khúc xạ ánh sáng

A. Bài tập ví dụ

Bài tập 1: Tia sáng đi từ nước có chiết suất \(\frac{4}{3}\) sang thuỷ tinh có chiết suất 1,5. Tính góc khúc xạ và góc lệch D tạo bởi tia khúc xạ và tia tới, biết góc tới i=30^o.

 

Phương pháp:

Muốn giải được bài tập này chúng ta sẽ điểm lại 2 kiến thức áp dụng vào bài toán là định luật khúc xạ ánh sáng và công thức tính góc lệch D.

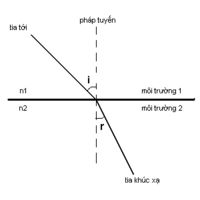
Định luật khúc xạ ánh sáng:

\(\frac{\sin i}{\sin r}=\frac{n_2}{n_1}\Leftrightarrow n_1.\sin i=n_2.\sin r\)

 

Trong đó:

• i: là góc tới.
• r: là góc khúc xạ.
• n₁: là chiết suất môi trường chứa tia tới.
• n₂: là chiết suất môi trường chứa tia khúc xạ.

Góc lệch D là góc lệch của tia ló so vói tia tới (xét về phương diện hướng truyền).

Khi ta đã nhớ được kiến thức trên thì bước vào giải bài toán thôi!!!

 

Đáp án:

Theo đề bài ta có được:

\(n_1=\frac{4}{3};\: n_2=1,5;\: i=30^o\)

Áp dụng định luật khúc xạ ánh sáng ta có:

\(n_1.\sin i=n_2.\sin r\Leftrightarrow 1,5.\sin 30^o=\frac{4}{3}.\sin r\Rightarrow r\approx 26,4^{o}\)

Góc lệch D tạo bởi tia khúc xạ và tia tới là:

\(D=i-r=30^o-26,4^o=3,6^o\)

 

Bài tập 2: Một tia sáng truyền từ môi trường A vào môi trường B dưới tới là 9^o thì góc khúc xạ là 8^o. 

a. Tìm góc khúc xạ khi góc tới là 60^o.

b. Tính vận tốc truyền ánh sáng trong môi trường A biết vận tốc ánh sáng trong môi trường B là 200 000 km/s.

 

Đáp án:

a. Do đề bài không cho chiết suất ánh sáng của môi trường A và B nên ta gọi chiết suất ánh sáng của môi trường A và B lần lượt là n_A, n_B.

Áp dụng định luật khúc xạ ánh sáng khi tia sáng truyền từ môi trường A vào môi trường B dưới góc tới là 9^o thì góc khúc xạ là 8^o, ta có:

\(n_A\sin 9^o=n_B\sin 8^o\) (1)

Khi tia sáng truyền với góc tới i = 60^o thì:

\(n_A\sin 60^o=n_B\sin r\) (2)

Lấy (2) chia cho (1) vế theo vế ta được:

\(\frac{\sin 60^o}{\sin 9^o}=\frac{\sin r}{\sin 8^o}\)

\(\Rightarrow \sin r=\sin 8^o\frac{\sin 60^o}{\sin 9^o}=0,77\)

\(\Rightarrow r=50,4^o\)

b. Muốn tính được vận tốc ánh sáng trong một môi trường bất kỳ ta cần biết mối liên hệ giữa chiết suất và vận tốc ánh sáng sau:

\(n=\frac{c}{v}\)

Dựa theo mối liên hệ trên ta được:

\(\left\{\begin{matrix} n_A = \frac{c}{v_A} \; \\ n_B=\frac{c}{v_B} \end{matrix}\right.\)

\(\Rightarrow \frac{n_B}{n_A}=\frac{v_A}{v_B}\Rightarrow v_A=\frac{n_B}{n_A}v_B=224805,6\: (km/s)\)

 

Bài tập 3: Hãy xác định giá trị của góc tới trong trường hợp sau:

a. Dùng tia sáng truyền từ thuỷ tinh và khúc xạ ra không khí. Biết tia khúc xạ và tia phản xạ ở mặt thuỷ tinh tạo với nhau góc 90^o. Chiết suất của thuỷ tinh là 1,5.

b. Tia sáng truyền từ nước và khúc xạ ra không khí. Tia khúc xạ và tia phản xạ ở mặt nước vuông góc với nhau. Nước có chiết suất \(\frac{4}{3}\). Xác định góc tới.

 

Đáp án:

a. Từ hình vẽ xét nửa mặt phẳng bên phải ta có:

(90^o – r) + (90^o – i) = 90^o

⇒ r + i =90^o ⇒ r = 90^o – i

Vận dụng định luật khúc xạ ánh sáng ta có:

\(n_1\sin i =n_2\sin r\)

\(\Leftrightarrow 1,5.\sin i =1.\sin (90^o-i)\Leftrightarrow 1,5.\sin i=1.\cos i\)

\(\Rightarrow \tan i=\frac{1}{1,5}\Rightarrow i\approx 33,7^o\)

b. Tương tự câu trên ta có:

\(\frac{4}{3}.\sin i=1.\sin (90^o-i)=\cos i\)

\(\Rightarrow \tan i=\frac{3}{4}\Rightarrow i\approx 37^o\)

B. Bài tập tự luyện

Bài tập 1: Một tia sáng đi từ không khí vào một khối chất có chiết suất \(n=\sqrt{2}\) với góc tới i = 45^o. Coi tốc độ ánh sáng khi truyền trong không khí là c = 2.10⁸ m/s.

a. Tính tốc độ của ánh sáng khi truyền trong khối chất này.

b. Tính góc khúc xạ.

c. Tính góc lệnh D tạo bởi tia khúc xạ và tia tới.

 Lời giải: Tại đây

 

Bài tập 2: Tia sáng đi từ không khí tới gặp mặt phân cách giữa không khí và môi trường trong suốt có chiết suất n với góc tới i.

a. Khi góc tới i = 45^o thì thấy góc hợp bởi tia khúc xạ và tia phản xạ là 105^o. Hãy tính chiết suất n của môi trường trong suốt nói trên.

b. Thay môi trường trên bằng một môi trường có chiết suất n = 1,5. Phải điều chỉnh góc tới đến giá trị nào thì góc tới gấp 2 lầ góc khúc xạ.

Lời giải: Tại đây

 

Bài tập 3: Một tia sáng được chiếu đến điểm chính giữa của mặt trên một khối lập phương trong suốt, chiết suất n = 1,5. Tìm góc tới lớn nhất để tia khúc xạ còn gặp đáy của khối lập phương.

Lời giải: Tại đây

Dạng 2: Lưỡng chất phẳng

A. Bài tập ví dụ

Bài tập 1: Mắt người và cá cùng cách mặt nước là 40 cm, cùng nằm trên một mặt phẳng vuông góc với mặt nước. Biết chiết suất của nước là \(n=\frac{4}{3}\). Hỏi người thấy cá cách mình bao xa?

Lời giải:

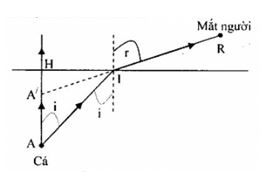
Gọi A là cá thật và A’ là ảnh của cá

Từ hình vẽ ta có:

\(\left\{\begin{matrix}\tan i=\frac{HI}{HA}\approx \sin i\approx i \\ \tan r= \frac{HI}{HA’} \approx \sin r \approx r \end{matrix}\right.\)

Theo định luật khúc xạ ánh sáng ta có:

\(n. \sin i=1. \sin r \Rightarrow \frac{\sin i}{\sin r}=\frac{1}{n}\)

\(\Leftrightarrow \frac{HA’}{HA}=\frac{1}{n}\Rightarrow HA’=\frac{HA}{n}=\frac{40}{\frac{4}{3}}=30(cm)\)

Vậy người nhìn thấy cá cách mình đoạn dài 40 + 30 = 70 cm

Bài trên là một ví dụ về lưỡng chất phẳng và chứng minh công thức tổng quát của dạng bài này. Vậy lưỡng chất phẳng là gì?

Sau đây ta sẽ tìm hiểu thế nào là lưỡng chất phẳng. 

     Lưỡng chất phẳng (LCP) là mặt phân cách giữa hai môi trường có chiết suất n_1^, n₂.

Công thức tổng quát cho trường hợp có LCP:

\(\frac{d_{anh}}{d_{vat}}=\frac{n_{kx}}{n_{toi}}\)

 

Bài tập 2: Trong một cái chậu có lớp nước dày 12 cm và một lớp benzen dày 9 cm nổi trên mặt nước. Một người nhìn vào chậu theo phương gần như thẳng đứng sẽthấy đáy chậu cách mặt thoáng bao nhiêu ? Vẽ đường đi của chùm tia sáng từmột điểm trên đáy chậu. Cho biết chiết suất của nước là n = 4/3 và của benzen là n’ = 1,5.

Lời giải:

Ở bài này ánh sáng sẽ truyền qua 3 môi trường rồi mới đến mắt người nhìn nên ta chia thành 2 giai đoạn sau:

Giai đoạn 1: Ánh sáng truyền từ đáy chậu qua lớp nước và đến lớp benzen

Áp dụng công thức tổng quát ta đã chứng minh ở bài trên ta có:

\(\frac{d_{anh}}{d_{vat}}=\frac{n_{kx}}{n_{toi}}\Leftrightarrow \frac{d_1}{d_0}=\frac{1,5}{\frac{4}{3}}\Rightarrow d_1=12.\frac{1,5}{\frac{4}{3}}=13,5(cm)\)

Giai đoạn 2: Ánh sáng truyền từ lớp benzen qua không khí và đến mặt thoáng

Tương tự ta có:

\(\frac{d_2}{d_1+9}=\frac{1}{1,5}\Rightarrow d_2=(13,5+9).\frac{1,5}{\frac{4}{3}}=15(cm)\)

Vậy người đó nhìn thấy đáy chậu cách mặt thoáng 1 đoạn 15 cm.

B. Bài tập tự luyện

Bài tập 1: Một chậu chứa một lớp nước dày 30 cm, chiết suất của nước là 4/3.

a. Chiều một chùm tia song song với mặt nước với góc tới 45^o. Tính góc lệch hợp bởi chùm tia khúc xạ và chùm tia tới.

b. Mắt ở trong không khí, nhìn xuống đáy chậu theo phương gần vuông góc với mặt nước sẽ thấy đáy chậu cách mặt nước một đoạn bao nhiêu?

Lời giải: Tại đây

 

Bài tập 2: Một bể nước cao h chứa đầy nước, một người đặt mắt sát mặt nước nhìn xuống đáy bể theo phương gần vuông góc với đáy bể thấy đáy bể dường như cách mắt mình 120 cm. Xác định h, cho chiết suất của nước là \(\frac{4}{3}\).

Lời giải: Tại đây

 

Bài tập 3: Một người ngồi trên bờ hồ nhúng chân vào nước trong suốt. Biết chiết suất của nước là \(\frac{4}{3}\). 

a. Khoảng cách thực từ bàn chân người đó đến mặt nước là 36 cm. Hỏi mắt người đó cảm thấy bàn chân cách nước bao nhiêu?

b. Người này cao 1,68 m, nhìn thấy một hòn sỏi dưới đáy hồ dường như cách mặt nước 1,5 m. Hỏi nếu đứng dưới hồ thì người ấy có bị ngập đầu không?

Lời giải: Tại đây