Chuyên đề: Suất điện động cảm ứng hiện tượng tự cảm

Dạng 3: Suất điện động cảm ứng trong một đoạn dây dẫn chuyển động

A. Bài tập ví dụ

Bài tập 1: Một thanh dẫn điện dài 20 cm tịnh tiến trong từ trường đều,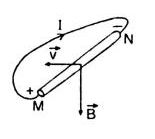 cảm ứng từ B = 5.10^-4 T. Vector vận tốc của thanh vuông góc với vector cảm ứng từ và có độ lớn bằng 5 m/s. Tính suất điện động cảm ứng trong thanh.

Phương pháp:

Ta cần nắm:

Cách tính suất điện động cảm ứng của một thanh kim loại bất kì
Các đại lượng và đơn vị của các đại lượng đó.

Công thức tính suất điện động cảm ứng:

$\left | \varepsilon \right |=Blvsin\alpha$

Trong đó:

- $\varepsilon$: là suất điện động cảm ứng (V).
- $B$: cảm ứng từ trong ống dây (hoặc thanh kim loại) (T).
- $l$: chiều dài của đoạn dây (m).
- $v$: vận tốc của đoạn dây (hoặc thanh kim loại) (m/s).
- $\alpha$: góc hợp bởi $\overrightarrow{v}$ và $\overrightarrow{B}$.

Đáp án:

Độ dài thanh l = 20 cm = 0,2 m.

Góc hợp bởi giữa vector vận tốc và vector cảm ứng từ là 90⁰. Suất điện động cảm ứng trong thanh là:

$\left | \varepsilon \right |=Blvsin90^{o}=0,08.0,2.7=0,112(V)$

Bài tập 2: Một thanh dẫn điện dài 20 cm được nối hai đầu của nó với hai đầu của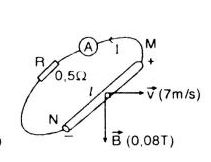 một đoạn mạch điện có điện trở 0,5 Ω. Cho thanh tịnh tiến trong từ trường đều cảm ứng từ B = 0,08 T với tốc độ 7 m/s. Hỏi số chỉ của ampe kế đặt trong mạch điện đó là bao nhiêu? Cho biết vector vận tốc của thanh vuông góc với các đường sức từ và điện trở của thanh rất nhỏ.

Đáp án

Độ dài thanh l = 20 cm = 0,2 m.

Thanh chuyển động vuông góc với các đường sức từ nên trong thanh xuất hiện suất động cảm ứng có độ lớn là:

$\left | \varepsilon \right |=Blvsin90^{o}=0,08.0,2.7=0,112(V)$

Thanh đóng vai trò như nguồn điện khi nối hai đầu với mạch ngoài. Dòng điện trong mạch điện khi đó là:

$I=\frac{\left | \varepsilon \right |}{R}=\frac{0,112}{0,5}=0,224(A)$

Vậy số chỉ của ampe kế đặt trong mạch là 0,224 A

Bài tập 3: Thanh MN chiều dài l = 40 cm quay đều quanh trục A và vuông góc với thanh trong từ trường đều B = 0,25 T làm thanh xuất hiện suất điện động cảm ứng E = 0,4 V.

a. Xác định các cực của thanh MN.

b. Xác định vận tốc góc của thanh.

Câu a:

Phương pháp:

Ta cần nắm rõ quy tắc bàn tay phải:

Đặt bàn tay phải hứng các đường sức từ, ngón cái choãi ra 90^o hướng theo chiều chuyển động của đoạn dây, khi đó đoạn dây dẫn đóng vai trò như một nguồn điện, chiều từ cổ tay đến bốn ngón tay chỉ chiều từ cực âm sang cực dương của nguồn điện đó.

Đáp án

Áp dụng quy tắc bàn tay phải vào hình ở đề bài ta được tay đặt như sau:

Ta được chiều dòng điện cảm ứng sẽ đi theo chiều từ M sang N. M sẽ là cực âm và N là cực dương.

Câu b:

Phương pháp:

Nhìn vào bài toán ta thấy nếu tính theo công thức đã được nêu ra ở bài 1 thì sẽ không được do ở đây vận tốc không phải chuyển động theo phương thẳng nào đó mà ở đây là vận tốc quay quanh 1 điểm cố định M. Chính vì lí do đó nên chúng ta cần dùng công thức tính suất điện động dựa theo độ biến thiên từ thông theo thời gian sau:

$\varepsilon =\frac{\Delta \Phi }{\Delta t}=\frac{B\Delta S.cos\alpha}{\Delta t}$

Trong đó:

- - $\Delta \Phi$: là độ biến thiên từ thông.
  - $B$: là cảm ứng từ (T).
  - $\Delta S$: khoảng diện tích quét được trong thời gian $\Delta t$.

Đáp án:

Khoảng diện tích trong thời gian $\Delta t$ quét được là:

$\Delta S=\pi l^{2}\frac{\Delta \phi }{2\pi}=\pi l^2\frac{\omega \Delta t}{2\pi }=\frac{l^2\omega }{2}\Delta t$ (1)

Độ biến thiên từ thông

$\Delta \Phi =B\Delta Scos\alpha=B\Delta S$ (vì $cos\alpha = 1$)

Suất điện động cảm ứng:

$\varepsilon =\frac{\Delta \Phi }{\Delta t}=\frac{B\Delta S}{\Delta t}$ (2)

Thay (1) vào (2) ta được:

$\varepsilon =\frac{Bl^2\omega }{2}\Rightarrow \omega =\frac{2E}{Bl^2}=\frac{2.0,4}{0,25.(0,4)^2}=20\: (rad/s)$

Bài tập 4: Hình ảnh nào xác định đúng chiều dòng điện cảm ứng trông đoạn dây dẫn chuyển động trong từ trường:

Lời giải:

Nhận thấy câu A là đáp án đúng.

Câu C đặt giống câu A nhưng do I = 0 nên đây là đáp án sai.

Câu B I xác định ngược lại so với chiều đúng.

Tương tự ở câu D cũng sai do I có chiều từ trong ra ngoài.

B. Bài tập tự luyện

Bài tập 1: Đặt khung dây ABCD cạnh một dây dẫn thẳng có dòng điện như hình sau:

Thanh AB có thể trượt trên thanh DE và CF. Điện trở R không đổi và bỏ qua điện trở của các thanh. AB song song với dòng điện thẳng và chuyển động thẳng đều với vận tốc vuông góc với AB. Xác định chiều của dòng điện cảm ứng trong mạch. Cho biết độ lớn của nó có thay đổi không?

Lời giải: Tại đây

Bài tập 2: Thanh kim loại dài 20 cm kéo trượt đều trên hai thanh ray kim loại nằm ngang như hình vẽ. Các dây nối với nhau bằng điện trở R = 3 Ω, vận tốc của thanh AB là 12 m/s. Hệ thống đặt trong từ trường đều có B = 0,4 T, Vecto B vuông góc với mạch điện.

a. Tìm suất điện động cảm ứng trong khung.

b. Cường độ dòng điện cảm ứng trong khung.

Lời giải: Tại đây

Bài tập 3: Cho mạch điện như hình vẽ, nguồn có suất điện động E = 1,5 V, r = 0,1 Ω. Thanh kim loại MN có chiều dài 1 m có điện trở R = 2,9 Ω. Từ trường B có phương thẳng đứng vuông góc với mặt khung như hình vẽ và B = 0,1T. Thanh MN dài có điện trở không đáng kể.

a. Ampe kế chỉ bao nhiêu khi MN đứng yên? Tính lực tác dụng lên thanh MN khi đó.

b. Ampe kế chỉ bao nhiêu khi MN di chuyển về phía phải với vận tốc v = 3 m/s sao cho hai đầu MN luôn tiếp xúc với hai thanh đỡ bằng kim loại? Tính độ lớn lực từ tác dụng lên thanh MN khi đó.

c. Muốn Ampe kế chỉ số 0 phải để thanh MN di chuyển về phía nào với vận tốc là bao nhiêu?

Lời giải: Tại đây

Dạng 4: Hiện tượng tự cảm

A. Bài tập ví dụ

Bài tập 1: Một ống dây dài l = 30 cm gồm N = 1000 vòng dây, đường kính mỗi vòng dây d = 8 cm có dòng điện với cường độ i = 2 A đi qua.

a. Tính độ tự cảm của ống dây.

b. Tính từ thông qua mỗi vòng dây.

c. Thời gian ngắt dòng điện là t = 0,1 s, tính suất điện động tự cảm xuất hiện trong ống dây.

Phương pháp:

Áp dụng công thức tính độ tự cảm:

$L=4\pi.10^{-7}.n^2.V$

Hoặc

$L=4\pi.10^{-7}.\frac{N^2}{l}.S$

- L: hệ số tự cảm (H)
- V: Thể tích của ống dây (m³)
- $n=\frac{N}{l}$: mật độ ống dây
- N: là số vòng dây
- l: chiều dài ống dây (m)
- S: tiết diện ống dây (m²)

Đáp án:

a. Độ tự cảm của ống dây là:

$L=4\pi.10^{-7}.\frac{N^2}{l}S=4\pi.10^{-7}.\frac{N^2}{l}.\frac{d^2}{4}\pi=\pi^{2}.10^{-7}.\frac{1000^2}{0,3}.0,08^2=0,021\: (H)$

b. Từ thông qua ống dây:

$\Phi =Li=0,021.2=0,042$

Từ thông qua mỗi vòng dây là:

$\Phi _{1}=\frac{\Phi }{N}=\frac{0,042}{1000}=4,2.10^{-5}$

c. Suất điện động tự cảm xuất hiện trong ống dây là:

$e_{tc}=L\frac{\Delta i}{\Delta t}=\frac{0,042}{0,1}=0,42$

Bài tập 2: Trong mạch điện như hình vẽ, cuộn cảm L có điện trở bằng không. Lúc đầu đóng khoá k về vị trí a để nạp năng lượng cho cuộn cảm L, khi đóng dòng điện qua L bằng 1,2 A. Chuyển K sang vị trí b, tính nhiệt lượng toả ra trong R. Biết độ tự cảm L = 0,2 H.

Lời giải:

Công thức tính năng lượng tích trữ trong L cũng chính là công thức tính năng lượng từ trường:

$L=\frac{1}{2}Li^2$

Năng lượng cuộn cảm L tích trữ được:

$W_L=\frac{1}{2}Li^2=\frac{1}{2}.0,2.(1,2)^2=0,144(J)$

Khi chuyển khoá K sang vị trí b thì toàn bộ năng lượng tích trữ trên cuộn cảm L sẽ chuyển sang toả nhiệt hết trên R. Nên nhiệt lượng toả ra trên R là 0,144 J.

Bài tập 3: Một ống dây dài được cuốn với mật độ 2000 vòng/mét. Ống dây có thể tích 500 cm³. Ống dây được mắc vào một mạch điện. Sau khi đóng công tắc dòng điện trong ống dây biến đổi theo thời gian như đồ thị sau. Lúc đóng công tắc ứng với thời điểm t = 0. Tính suất điện động tự cảm trong ống dây trong hai TH sau:

a. Sau khi đóng công tắc với thời điểm t = 0,05 s.

b. Từ thời điểm t = 0,05 s trở về sau.

Lời giải:

a. Độ tự cảm của ống dây:

$L=4\pi.10^{-7}.n^2.V\approx 2,51.10^{-3}$

Trong khoảng thời gian từ 0 đến 0,05 s dòng điện tăng từ i₁ = 0 A đến i₂ = 5 A

Suất điện động tự cảm trong thời gian này:

$\left | e_{tc} \right |=L\left | \frac{\Delta i}{\Delta t} \right |\approx 0,25(V)$

b. Từ sau thời điểm t = 0,05 s dòng điện không đổi nên $\Delta i=0\Rightarrow e_{tc}=0$

B. Bài tập tự luyện

Bài tập 1: Một ống dây điện có lõi bằng vật liệu sắt từ có độ từ thẩm là μ = 10⁴, cảm ứng từ bên trong ống dây là B = 0,05 T. Tính mật độ năng lượng từ trường trong ống dây.

Lời giải: Tại đây

Bài tập 2: Cho mạch điện như hình vẽ, L = 1 H, E = 12 V, r = 0 điện trở của biến trở là 10 Ω. Điều chỉnh biến trở về trong 0,1 s điện trở của biến trở giảm còn 5 Ω.