1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng:

(a) Khoảng cách từ một điểm đến một đường thẳng: Cho O và đường thẳng d, H là hình chiều của O lên d. Độ dài của đoạn thẳng OH gọi là khoảng cách từ điểm O đến đường thẳng d. OH bé nhất so với tất cả các khoảng cách từ O đến mọi điểm trên A.

Trong hình trên, đường thẳng a chính là đường thẳng d trong định nghĩa.

(b) Khoảng cách từ một điểm đến một mặt phẳng: Cho điểm O và mặt phẳng (P), H là hình chiếu của O lên (P). Độ dài đoạn thẳng OH gọi là khoảng cách từ điểm O đến mặt phẳng (P). OH là bé nhất so với tất cả các khoảng cách từ O đến mọi điểm trên mặt phẳng (P).

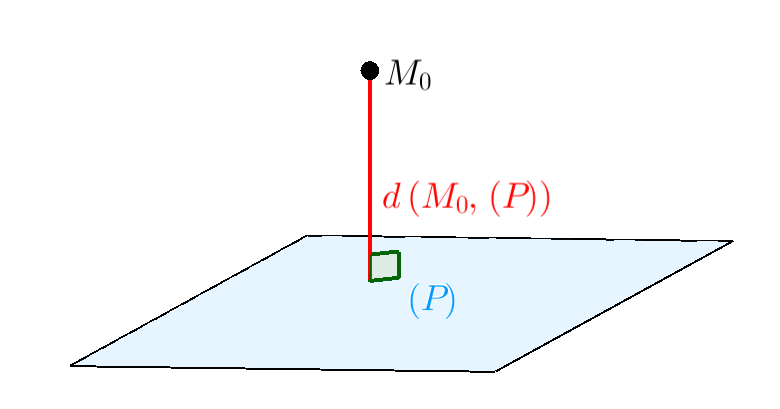
Trong hình trên, điểm M0 chính là điểm O.

2. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song:

1. Khoảng cách giữa đường thẳng và mặt phẳng song song:

Cho đường thẳng d và mặt phẳng (P) song song nhau. Khoảng cách giữa d và (P) là khoảng cách từ một điểm O thuộc d đến mặt phẳng (P).

2. Khoảng cách giữa hai mặt phẳng song song:

Cho hai mặt phẳng (P) và (Q) song song với nhau. Khoảng cách giữa (P) và (Q) là khoảng cách từ một điểm trên (P) đến (Q) (hoặc một điểm trên (Q) đến (P)).

3. Đường vuông góc chung và khoảng cách giữa hai đường thẳng chéo nhau:

1. Định nghĩa:

Đường thẳng d cắt hai đường thẳng a, b chéo nhau và cùng vuông góc với mỗi đường thẳng ấy được gọi là đường vuông góc chung của a và b.

Nếu đường vuông góc chung d cắt hai đường thẳng chéo nhau a và b lần lượt tại M, N thì độ dài đoạn thẳng MN gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.

Từ định nghĩa, ta có các nhận xét sau:

2. Nhận xét:

Nhận xét 1. Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó đồng thời chứa đường thẳng còn lại.

Nhận xét 2. Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứ hai đường thẳng đó.

Nhận xét 3. Khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách bé nhất so với khoảng cách giữa hai điểm bất kì lần lượt lấy trên a và b.

4. Một số bài tập đề nghị:

Tác giả xin đề nghị một số bài tập sau:

Bài 1. Cho hình chóp S.ABC, có SA = a, SB = b, SC = c và SA, SB, SC đôi một vuông góc nhau. Tính khoảng cách từ S đến mặt phẳng (ABC).

Bài 2. Cho tứ diện đều ABCD có cạnh a.

(a) Tính khoảng cách từ A đến BC.

(b) Tính khoảng cách từ A đến (BCD).

Bài 3. Cho hình hộp chữ nhật ABCD.XYZT có đáy là hình vuông cạnh a, chiều cao AX = 2a.

(a) Tính khoảng cách từ A đến (BDTY).

(b) Tính khoảng cách từ T đến (DXZ).

Bài 4. Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, SA vuông góc với (ABC). Biết AC = 2a, SA = a. Gọi M, N, P lần lượt là trung điểm AB, BC, SB.

(a) Chứng minh MP // (SAC). Tính khoảng cách từ MP đến (SAC).

(b) Chứng minh (MNP) // (SAC). Tính khoảng cách từ (MNP) đến (SAC).

Bài 5. Cho hình lăng trụ đứng ABC.XYZ có đáy là tam giác ABC đều cạnh a. Cạnh bên YC tạo với mặt (AXZC) một góc 30 độ.

(a) Tính khoảng cách giữa hai đáy của hình trụ.

(b) Gọi N là trung điểm YZ. I là trung điểm XC. Tính khoảng cách giữa NI với (ABYX).

Bài 6. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD), SA = 2a. Gọi M, N, P lần lượt là trung điểm SB, SC, SD. Tính khoảng cách giữa các cặp đường thẳng:

(a) SD và BC.

(b) BD và SC.

(d) MP và AC.

Bài 7. Cho hình hộp chữ nhật ABCD.XYZT có AB = 3, AD = 5, AX = 6.

(a) Tính khoảng cách giữa XD và BZ.

(b) Tính khoảng cách giữa CD và BT.

Bài 8. Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Gọi M, N lần lượt là trung điểm của AA’ và BB’. Tính khoảng cách giữa hai đường thẳng B’M và CN.