Bài 1+2: Khối đa diện

Khái niệm về khối đa diện

Định nghĩa hình đa diện

Hình đa diện là hình được tạo bởi một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện:

Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.

Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.

Hình (H) gồm các đa giác đó được gọi là một hình đa diện, hoặc đa diện.

Ví dụ:

Định nghĩa khối đa diện

Hình (H) cùng với các điểm nằm trong (H) được gọi là khối đa diện giới hạn bởi hình (H).

Mỗi đa giác của hình (H) được gọi là một mặt của khối đa diện.

Các đỉnh, cạnh của mỗi mặt còn gọi là đỉnh, mặt của khối đa diện.

Khối chóp và khối lăng trụ

Khối đa diện được gọi là khối chóp, khối chóp cụt nếu nó được giới hạn bới một hình chóp, hình chóp cụt.

Khối đa diện được gọi là khối lăng trụ nếu nó được giới hạn bởi một hình lăng trụ

Phân chia và lắp ghép các khối đa diện

Cho khối chóp tứ giác S.ABCD. Xét hai khối chóp tam giác S.ABC và S.ACD, ta nhận thấy:

Hai khối chóp đó không có điểm chung (các điểm trong của khối chóp này không thuộc khối chóp kia và ngược lại)
Hợp của hai khối chóp S.ABC và S.ACD là khối chóp S.ABCD

Khi đó ta nói:

Khối đa diện S.ABCD được phân chia thành hai khối đa diện S.ABC và S.ACD

Cho khối lăng trụ ABC.A’B’C’. Mặt phẳng (AB’C’) chia khối lăng trụ thành hai khối đa diện gồm khối chóp tam giác AA’B’C’ và khối chóp tứ giác A.BB’C’C.

Tổng quát:

Mọi khối tứ diện và khối lăng trụ đều có thể được chia thành các khối đa diện.

Phép đối xứng qua mặt phẳng và sự bằng nhau của các khối đa diện

Phép biến hình trong không gian

Phép biến hình F trong không gian là một quy tắc để với mỗi điểm M xác định được một điểm M’ duy nhất gọi là ảnh của điểm M qua phép biến hình F

Ta còn nói F biến điểm M thành điểm M’ và kí hiệu M’=F(M)

Qua phép biến hình F mỗi hình (H) được biến thành hình (H’) gồm tất cả các ảnh của các điểm thuộc hình (H).

Phép đối xứng qua mặt phẳng

Định nghĩa

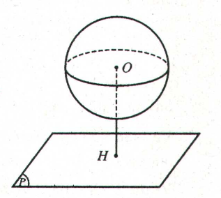
Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó và biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của MM’.

Định lí

Nếu phép đối xứng qua mặt phẳng (P) biến hai điểm M, N lần lượt thành hai điểm M’, N’ thì M’N’=MN.

Kết luận:

Phép đối xứng qua mặt phẳng là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.

Mặt phẳng đối xứng của một hình

Định nghĩa

Nếu phép đối xứng qua mặt phẳng (P) biến hình (H) thành chính nó thì (P) gọi là mặt phẳng đối xứng của hình (H).

Ví dụ: Cho tứ diện đều ABCD. Gọi M là trung điểm của cạnh CD thì phép đối xứng qua (ABM) biến A thành A, B thành B, C thành D, D thành C. Như vậy phép đối xứng đó biến tứ diện ABCD thành chính nó, suy ra mặt phẳng (ABM) là mặt phẳng đối xứng của tứ diện ABCD.

Mặt phẳng đối xứng của một số hình thường gặp

Hình hộp chữ nhật có 3 kích thước khác nhau: có 3 mặt phẳng đối xứng.

Hình lăng trụ tam giác đều: có 4 mặt phẳng đối xứng.

Hình chóp tam giác đều (cạnh bên và đáy không bằng): có 3 mặt phẳng đối xứng.

Tứ diện đều: có 6 mặt phẳng đối xứng.

Hình chóp tứ giác đều: có 4 mặt phẳng đối xứng.

Hình bát diện đều: có 9 mặt phẳng đối xứng.

Hình lập phương: có 9 mặt phẳng đối xứng.

Phép dời hình và sự bằng nhau của các hình

Phép dời hình

Định nghĩa

Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý. Tức là nếu F biến hai điểm A, B bất kì lần lượt thành hai điểm A’, B’ thì $A'B'=AB$ .

Tính chất

Phép dời hình biến một đa diện thành một đa diện, biến các đỉnh, cạnh, mặt của đa diện thành đỉnh, cạnh, mặt tương ứng của đa diện tương ứng.

Một số ví dụ về phép dời hình

Phép tịnh tiến

Phép tịnh tiến theo vecto $\vec{v}$ là phép biến hình biến điểm M thành M’ sao cho $\overrightarrow{MM'}=\vec{v}$ .

Phép đối xứng trục

Phép đối xứng trục là phép đối xứng qua đường thẳng d biến hình mọi điểm thuộc d thành chính nó, biến điểm M không thuộc d thành điểm M’ sao cho d là trung trực của MM’.

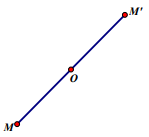
Phép đối xứng tâm

Phép đối xứng tâm O là phép biến hình biến điểm O thành chính nó, biến điếm M khác O thành điểm M’ sao cho O là trung điểm của MM’.

Hai hình bằng nhau

Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

Phép vị tự trong không gian và hai hình đồng dạng

Phép vị tự trong không gian

Định nghĩa

Cho số k không đổi khác 0 và một điểm O cố định. Phép biến hình trong không gian biến mỗi điểm M thành M’ sao cho $\overrightarrow{OM'}=k\overrightarrow{OM}$ gọi là phép vị tự. Điểm O gọi là tâm vị tự, k là tỉ số vị tự

Tính chất

Nếu phép vị tự tỉ số k biến hai điểm M, N thành hai điểm M’, N’ thì $\overrightarrow{M'N'}=k\overrightarrow{MN}$ và do đó $M'N'=\left | k \right |MN$ .

Phép vị tự biến ba điểm thẳng hàng thành ba điểm thẳng hàng, bốn điểm đồng phẳng thành bốn điểm đồng phẳng.

Hai hình đồng dạng

Hình (H) được gọi là đồng dạng với hình (H’) nếu có một phép vị tự biến hình (H) thành hình $(H_1)$ đồng dạng với hình (H’).

Khối đa diện lồi và khối đa diện đều

Khối đa diện lồi

Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn luôn thuộc (H)

Khối đa diện đều

Khối đa diện đều là khối đa diện lồi thỏa mãn 2 tính chất sau:

Mỗi mặt là một đa giác đều $p$ cạnh

Mỗi đỉnh của nó là đỉnh chung của đúng $q$ mặt.

Khối đa diện đều như vậy được gọi là khối đa diện đều loại $\left \{ p;q \right \}$

Có năm loại khối đa diện đều là: $\left \{ 3;3 \right \},\left \{ 4;3 \right \},\left \{ 3;4 \right \},\left \{ 5;3 \right \},\left \{ 3;5 \right \}$

Đa diện đều cạnh $a$	Loại	Đỉnh	Cạnh	Mặt	$V$	Bán kính mặt cầu ngoại tiếp
Tứ diện đều	$\left \{ 3;3 \right \}$	4	6	4	$\frac{\sqrt2}{12}a^3$	$\frac{\sqrt6}{4}a$
Lập phương	$\left \{ 4;3 \right \}$	8	12	6	$a^3$	$\frac{\sqrt3}{2}a$
Bát diện đều	$\left \{ 3;4 \right \}$	6	12	8	$\frac{\sqrt2}{3}a^3$	$\frac{\sqrt2}{2}a$
Mười hai mặt đều	$\left \{ 5;3 \right \}$	20	30	12	$\frac{15+7\sqrt5}{12}a^3$	$\frac{\sqrt3+\sqrt{15}}{4}a$
Hai mươi mặt đều	$\left \{ 3;5 \right \}$	12	30	20	$\frac{15+5\sqrt5}{12}a^3$	$\frac{\sqrt{10}+\sqrt{20}}{4}a$