1. Lí thuyết:

1. Khối nón:

Đối với khối nón, ta có các công thức cần nhớ sau: Cho khối nón có bán kính đáy R, chiều cao h, đường sinh l.

• Thể tích khối nón:
• Diện tích xung quanh:
• Diện tích toàn phần:
• Công thức đường sinh:

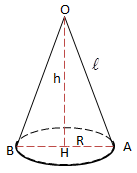
2. Xác định thiết diện của khối nón bị cắt bởi một mặt phẳng:

1. Nếu mặt phẳng cắt đi qua đỉnh của khối nón thì thiết diện là một tam giác cân.
2. Nếu mặt phẳng cắt vuông góc với trục của khối nón thì thiết diện là một hình tròn.
3. Nếu mặt phẳng cắt song song với trục của khối nón thì thiết diện là một hình giới hạn bởi một hyperbol.
4. Nếu mặt phẳng cắt song song với đường sinh của khối nón thì thiết diện là một hình giới hạn bởi một parabol.
5. Nếu mặt phẳng cắt không song song với đường sinh hay trục của khối nón thì thiết diện là một hình elip.

3. Khối trụ:

Tương tự, ta cũng có một số công thức cần nhớ đối với khối trụ: Cho khối trụ có bán kính đáy R, chiều cao h.

• Thể tích khối trụ:
• Diện tích xung quanh:
• Diện tích toàn phần:

2. Một số ví dụ:

Bài 1. Cho khối nón có thiết diện qua trục là tam giác vuông cân, cạnh huyền bằng .

(a) Tính diện tích xung quanh và diện tích toàn phần của khối nón.

(b) Tính thể tích của khối nón.

Giải

Từ các giả thiết của đề bài, ta có thể suy ra những dữ kiện sau: (R: bán kính, h: đường cao, l: đường sinh)

• R = .
• h = .
• l = a.

Áp dụng công thức tính diện tích xung quanh, suy ra diện tích xung quanhh sẽ bằng

Diện tích toàn phần vì thế sẽ bằng:

(b) Thể tích của khối nón =  Thay R, h vào, ta tính được thể tích khối nón là

Bài 2 (hay!). Cho tam giác vuông OAB có OA + OB = c (c là một hằng số không đổi). Xoay tam giác vuông OAB quanh cạnh OA tạo thành một khối nón. Tính thể tích lớn nhất của khối nón đó.

Áp dụng công thức V =

Lưu ý. Để làm những dạng toán thế này, cần có kiến thức về bất đẳng thức Cauchy (hay còn gọi là bất đẳng thức AM – GM).

2. Bài tập áp dụng:

Bài 1. Cho khối nón có bán kính đáy là R, đỉnh S. Góc tạo bởi đường cao và đường sinh là 60 độ.

(a) Tính diện tích thiết diện cắt khối nón theo hai đường sinh vuông góc với nhau.

(b) Tính diện tích xung quanh và thể tích của khối nón.

Bài 2. Cho tam giác ABC vuông tại A có AB = , AC = a. Tính diện tích xung quanh của hình nón tròn xoay tạo thành khi quay tam giác ABC quanh đường thẳng AB.

Bài 3. Cho hình chóp đều có tất cả các cạnh bên đều bằng nội tiếp một hình nón. Tính thể tích V của khối nón được tạo nên bởi hình nón trên.

Bài 4. Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh a. Tính thể tích của khối trụ.

Bài 5. Một hình trụ có thiết diện qua trục là hình vuông cạnh a. Tính thể tích V của hình trụ đó.

Bài 6. Cắt một khối trụ tròn xoay bởi một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng 2a. Tính diện tích toàn phần của khối trụ.

Bài 7. Cho hình nón có diện tích toàn phần bằng và bán kính đường tròn đáy bằng 3. Tính thể tích V của khối nón.