Định nghĩa
Cho
Số thực thỏa mãn
được gọi là logarit cơ số a của b kí hiệu là
, nghĩa là
Trong đó:
b: biểu thức tính log (b>0)
a: cơ số ()
: giá trị của log
Ví dụ 1: Tính
Bài giải
Chú ý: Với và
ta luôn có:
Ví dụ 2:
a. Tính
b. Tìm x biết
Bài giải
a.
b.
Tính chất
Cho b,c>0, ta có:
Chứng minh:
Đặt
Xét a>1, ta có:
(do a>1)
(đpcm)
Xét 0<a<1, ta có:
(do 0<a<1)
(đpcm)
Các quy tắc tính logarit
Các công thức cơ bản
Định lí
Cho , ta có:
Trường hợp là số nguyên chẵn và chưa biết dấu của b thì ta sử dụng công thức:
Chẳng hạn:
Chứng minh:
Đặt , ta có:
Hệ quả
Cho và
, ta có
Ví dụ 3: Tính giá trị biểu thứ
Bài giải
Nhóm đổi cơ số
Định lí
Cho và
, ta có:
hay
Chứng minh:
Đặt
Ta có:
(đpcm)
Hệ quả
- Với
và
, ta có:
hay
- Với
và
và
, ta có:
- Với
và
, ta có:
Chứng minh:
(đúng theo nội dung định lí)
Ví dụ 4: Rút gọn biểu thức
Bài giải
Ghi chú
Với x>0, logarit cơ số 10 của x được gọi là logarit thập phân của x. Kí hiệu:
Với x>0, logarit cơ số e của x được gọi là logarit tự nhiên của x (logarit napier của x). Kí hiệu: . Trong đó e là hằng số và
Bài tập
- Tính
- Tính
- Cho
là các số thực dương và
. Tính
theo
.
- Cho
. Tính
theo
và
- Cho
. Tính
.
- Chứng minh:
- Cho
và
. Tính giá trị của biều thức
- Cho
và
. Tính giá trị biểu thức
- Cho
và
. TÍnh giá trị biểu thức
.
- Chứng minh:
- Cho
thỏa
. Khẳng định nào đúng?
- Cho
thỏa
. Tìm
- Cho
thỏa mãn
. Tính tỉ số
- Cho
là số nguyên dương. Tính
- Tính
- Đặt
. Biểu diễn
theo
và
- Cho
thỏa mãn
. Giá trị
bằng?
- Cho
. Tính
- Cho hàm số
với
. Biết
, hỏi giá trị của
- Cho hàm số
với
. Biết
, tính giá trị của
với
.







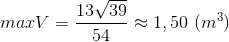
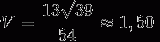
No Comments
Leave a comment Cancel