Phương trình lượng giác cơ bản
Phương trình lượng giác có dạng sinx = a
Để giải phương trình lượng giác dạng này, ta thực hiện theo các bước sau:
- Nếu \( \left | a \right |>1 \) thì phương trình vô nghiệm.
- Nếu \( \left | a \right |\leq 1 \) thì chọn một cung \( \alpha \) sao cho \( sin\alpha =a. \)
Vậy ta có \( sin\alpha = sinx \).
Vậy có 2 nghiệm x thỏa mãn: \( x=\alpha +k2r, x=\pi -\alpha +k2r(k\in \mathbb{Z}). \)
Phương trình lượng giác có dạng cosx = a
Để giải phương trình lượng giác dạng này, ta thực hiện theo các bước sau:
- Nếu \( \left | a \right |>1 \) thì phương trình vô nghiệm.
- Nếu \( \left | a \right |\leq 1 \) thì chọn một cung \( \alpha \) sao cho
- \( cos\alpha = a. \)
Vậy ta sẽ có \( cos\alpha = cosx \).
Vậy có 2 nghiệm x sẽ thỏa mãn: \( x = \alpha +k2\pi , x = -\alpha +k2\pi (k\in \mathbb{Z}). \)
Phương trình lượng giác có dạng tanx = a
Đối với phương trình lượng giác này sẽ đơn giản hơn 2 phương trình lượng giác ở phía trên.
Ta sẽ chọn cung \( \alpha \) sao cho \( tan\alpha = a. \)
Khi đó: \( tanx = tan\alpha \Leftrightarrow x = \alpha = k\pi (k\in \mathbb{Z}). \)
Phương trình lượng giác có dạng cotx = a
Cũng cách làm tương tự, ta sẽ chọn cung \( \alpha \) sao cho \( cot\alpha = a. \)
Khi đó: \( cotx = cot\alpha \Leftrightarrow x = \alpha +k\pi (k\in Z). \)
Bài tập tự luyện
Tác giả xin đề nghị một số bài tập tự luyện như sau:
Bài 1.
(a) 2sinx = – 1.
(b) sin3x = 1.
Bài 2.
(a) sin(x + 2) =
(b) \( cot(\frac{\pi }{5}-3x)=\frac{1}{3}. \)
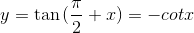
No Comments
Leave a comment Cancel