Tính chất của hàm số
1. Hàm số chẵn, hàm số lẻ:
- Hàm số y = f(x) có tập xác định D gọi là hàm số chẵn khi:
- Với mọi \( x \in D \) thì \( -x \in D \)
- f(x) = f(-x)
- Đồ thị hàm số chẵn đối xứng qua trục tung.
- Hàm số y = f(x) có tập xác định D gọi là hàm số lẻ khi:
- Với mọi \( x \in D \) thì \( -x \in D \)
- -f(x) = f(-x)
- Đồ thị hàm số lẻ đối xứng qua gốc tọa độ.
2. Hàm số đơn điệu
- Cho f(x) xác định trên tập (a;b) ⊂ ℝ:
- y = f(x) đồng biến trên (a;b) nếu với mọi x1, x2 ∈ (a;b) có x1 < x2 ⇒ f(x1) < f(x2).
- y = f(x) nghịch biến trên (a;b) nếu với mọi x1, x2∈ (a;b) có x1 < x2 ⇒ f(x1) > f(x2).
3. Hàm số tuần hoàn
- Hàm số y = f(x) xác định trên tập hợp D được gọi là hàm số tuần hoàn nếu tồn tại số T ≠ 0 sao cho với mọi x ∈ D, ta có:
- Khi đó, T được gọi là chu kì tuần hoàn của hàm số f(x)
Hàm số lượng giác
1. Hàm số sin
- Quy tắc đặt tương ứng mỗi số thực x với sin của góc lượng giác có số đo radian bằng x được gọi là hàm số sin
- Kí hiệu y = sinx
- Tập xác định: D = ℝ
- Tập giá trị là [-1;1]
- Là hàm số lẻ (do sin(-x) = -sinx)
- Là hàm số tuần hoàn với chu kì 2π
- Đồng biến trên mỗi khoảng
(\( \frac{- π}{2} \) + k 2 π ; \( \frac{ π}{2} \) + k 2 π ) và nghịch biến trên mỗi khoảng( \( \frac{ π}{2} \) + k 2 π ; \( \frac{3 π}{2} \) + k 2 π ) , vớik ∈ ℤ - Có đồ thị là một đường hình sin và nhận gốc tọa độ làm tâm đối xứng

Đồ thị hàm số y=sinx
2. Hàm số cosin
- Quy tắc đặt tương ứng mỗi số thực x với cos của góc lượng giác có số đo radian bằng x được gọi là hàm số cos
- Kí hiệu y = cosx
- Tập xác định: D = ℝ
- Tập giá trị là [-1;1]
- Là hàm số chẵn (do cos(-x) = cosx)
- Là hàm số tuần hoàn với chu kì 2π
- Đồng biến trên mỗi khoảng
( – π + k 2 π ; k 2 π ) - Có đồ thị là một đường hình sin và nhận trục tung làm trục đối xứng

Đồ thị hàm số y=cosx
3. Hàm số tan
- Quy tắc đặt tương ứng mỗi số thực x ∈ ℝ\{π2+kπ; k ∈ℤ} với tan của góc lượng giác có số đo radian bằng x được gọi là hàm số tan
- Kí hiệu y=tanx
- Tập xác định:
D = ℝ \ { π 2 + k π ; k ∈ ℤ. - Tập giá trị là ℝ
- Là hàm số lẻ (do tan(-x) = -tanx)
- Là hàm số tuần hoàn với chu kì π
- Đồng biến trên mỗi khoảng
( – π 2 + k π ; π 2 + k π ), với k ∈ ℤ - Đồ thị nhận gốc tọa độ làm tâm đối xứng và nhận mỗi đường
x = π 2 + k π (k∈ℤ) làm một đường tiệm cận

Đồ thị hàm số y=tanx
4. Hàm số cot
- Quy tắc đặt tương ứng mỗi số thực x∈ ℝ\{kπ; k ∈ℤ} với cot của góc lượng giác có số đo radian bằng x được gọi là hàm số cot
- Kí hiệu y = cotx
- Tập xác định:
D = ℝ \ { k π ; k ∈ ℤ } - Tập giá trị là ℝ
- Là hàm số lẻ (do cot(-x) = -cotx)
- Là hàm số tuần hoàn với chu kì π
- Nghịch biến trên mỗi khoảng (kπ;π+kπ) với k ∈ ℤ
- Đồ thị nhận gốc tọa độ làm tâm đối xứng và nhận mỗi đường x=kπ (k∈ℤ) làm một đường tiệm cận

Đồ thị hàm số y=cotx
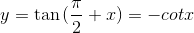









No Comments
Leave a comment Cancel