Ôn tập chương 3

Trong bài này ta sẽ tổng hợp tất cả kiến thức đã học ở chương 3, hình không gian của lớp 11. Chương 3 ta học về Vector trong không gian và quan hệ vuông góc. Đây là chương cuối cùng trong chương trình hình học lớp 11 và tạo tiền đề cực kì quan trọng để học hình học không gian lớp 12.

1. Vector trong không gian:

Trong không gian, ta cần nhớ các phép tính vector sau:

a) Qui tắc hình bình hành:

Nếu ABCD là hình bình hành thì ta có: $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}.$ (hình)

b) Qui tắc ba điểm:

Cho 3 điểm A, B, C bất kì thì ta luôn có: $\overrightarrow{AB} +\overrightarrow{BC}=\overrightarrow{AC}.$

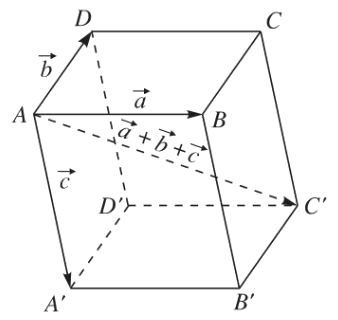
c) Qui tắc hình hộp:

Cho hình hộp ABCD.A’B’C’D’ thì ta luôn có $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}.$

Đồng thời, ta gần ghi nhớ các điều kiện để vector cùng phương và vector đồng phẳng.

d) Hệ thức trung điểm đoạn thẳng: Cho I là trung điểm của đoạn thẳng AB, O tùy ý. Ta có các hệ thức cần nhớ sau:

$\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0},\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OI}.$

e) Hệ thức trọng tâm của tam giác: Cho G là trọng tâm tam giác ABC, O tùy ý. Ta lại có hai hệ thức cần nhớ sau:

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0},\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}.$

f) Hệ thức trọng tâm tứ diện: Cho G là trọng tâm của tứ diện ABCD, O tùy ý. Ta có các hệ thức sau:

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0},\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=4\overrightarrow{OG}.$

g) Điểm M chia đoạn thẳng AB theo tỉ số k, O tùy ý. Ta có các hệ thức sau:

$\overrightarrow{MA}=k\overrightarrow{MB},\overrightarrow{OM}=\frac{\overrightarrow{OA}-k\overrightarrow{OB}}{1-k}.$

h) Điều kiện để hai vector cùng phương: $\overrightarrow{a},\overrightarrow{b}$ cùng phương (với vector a khác 0) tương đương với việc tồn tại duy nhất số k là số thực sao cho $\overrightarrow{b}=k\overrightarrow{a}.$

2. Sự đồng phẳng của ba vector:

Ba vector được gọi là đồng phẳng nếu chúng cùng song song với một mặt phẳng.
Điều kiện để ba vector đồng phẳng:
Cho ba vector $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ , trong đó $\overrightarrow{a},\overrightarrow{b}$ không cùng phương.
Khi đó: ba vector $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ đồng phẳng khi và chỉ khi tồn tại duy nhất m, n là các số thực sao cho $\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}.$
Cho ba vector không đồng phẳng $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ và vector $\overrightarrow{x}.$ tùy ý. Khi đó tồn tại duy nhất m, n, p là các số thực sao cho $\overrightarrow{x}=m\overrightarrow{a}+n\overrightarrow{b}+p\overrightarrow{c}.$

3. Góc giữa hai vector:

Cho $\overrightarrow{u},\overrightarrow{v}$ là hai vector trong không gian. Từ một điểm A bất kì, vẽ $\overrightarrow{AB}=\overrightarrow{u},\overrightarrow{AC}=\overrightarrow{v}.$ Vậy góc BAC ( $0^0\leq \widehat{BAC}\leq 180^0.$ ) là góc giữa hai vector $\overrightarrow{u},\overrightarrow{v}.$ , kí hiệu là $(\overrightarrow{u},\overrightarrow{v})=\widehat{BAC}.$

4. Tích vô hướng của hai vector:

Tích vô hướng của hai vector là kiến thức mà các bạn đã được giới thiệu vào năm lớp 10. Ta có định nghĩa của tích vô hướng như sau:

Định nghĩa. Tích vô hướng của hai vector $\overrightarrow{u},\overrightarrow{v}$ khác vector không là một số được kí hiệu là $\overrightarrow{u}.\overrightarrow{v}$ , xác định bởi công thức sau:

$\overrightarrow{u}.\overrightarrow{v}=\left | \overrightarrow{u} \right |.\left | \overrightarrow{v} \right |.cos(\overrightarrow{u},\overrightarrow{v})$

Trong trường hợp $\overrightarrow{u}=\overrightarrow{0}$ hoặc $\overrightarrow{v}=\overrightarrow{0}$ thì ta qui ước $\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{0}$ .

Đối với tích vô hướng của hai vector, ta có những tính chất như sau:

Tính chất. Với ba vector $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ và với mọi số k, ta có:

Tính chất giao hoán: $\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}$
Tính chất phân phối: $\overrightarrow{a}.(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}$
Tính chất với số k: $(k.\overrightarrow{a}).\overrightarrow{b}=k.(\overrightarrow{a}.\overrightarrow{b})=(k.\overrightarrow{b}).\overrightarrow{a}$
$(\overrightarrow{a})^2\geq 0,(\overrightarrow{a})^2=0\Rightarrow \overrightarrow{a}=\overrightarrow{0}.$

Lưu ý. Ta có thể ứng dụng tích vô hướng để tính góc giữa hai vector (dựa vào cos theo công thức tích vô hướng).

Ví dụ 1. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và AD, biết AB = CD = a, $MN=\frac{a\sqrt{3}}{2}.$

Tính góc giữa hai đường thẳng AB và CD.

Nếu làm một cách truyền thống, ta có thể xử lí bài này như sau:

Cách 1. Gọi I là trung điểm AC. Đặt $\widehat{MIN}=\alpha .$

Xét tam giác IMN có $IM=\frac{AB}{2}=\frac{a}{2},IN=\frac{CD}{2}=\frac{a}{2},MN=\frac{a\sqrt{3}}{2}.$

Theo định lí cos trong tam giác, ta có:

$cos\alpha =\frac{IM^2+IN^2-MN^2}{2IM.IN}=\frac{(\frac{a}{2})^2+(\frac{a}{2})^2-(\frac{a\sqrt{3}}{2})^2}{2.\frac{a}{2}.\frac{a}{2}}=-\frac{1}{2}<0$

$\Rightarrow \widehat{MIN}=120^0\Rightarrow (AB,CD)=60^0.$

Ta lưu ý rằng góc giữa hai đường thẳng luôn là góc nhọn (theo qui ước) và không bao giờ là góc tù.

Ngoài ra, ta còn có thể xử lí bài này theo cách như sau:

Cách 2. Xử lí bằng tích vô hướng của hai vector.

Ta có:

$cos(AB,CD)=cos(IM,IN)=\frac{\left | \overrightarrow{IM}.\overrightarrow{IN} \right |}{\left | \overrightarrow{IM} \right |.\left | \overrightarrow{IN} \right |}$

Lại có:

$\overrightarrow{MN}=\overrightarrow{IN}-\overrightarrow{IM}\Rightarrow (\overrightarrow{MN})^2=(\overrightarrow{IN}-\overrightarrow{IM})^2=IM^2+IN^2-2\overrightarrow{IM}.\overrightarrow{IN}$

$\Rightarrow \overrightarrow{IN}.\overrightarrow{IM}=\frac{IM^2+IN^2-MN^2}{2}=-\frac{a^2}{8}.$

Từ đây ta suy ra:

$cos(AB,CD)=\left | cos(IM,IN) \right |=\frac{1}{2}.$

Vậy $(AB,CD)=60^0.$

5. Vector chỉ phương của đường thẳng:

$\overrightarrow{a}\neq 0$ là vector chỉ phương của d nếu giá của vector a song song hoặc trùng với d.

6. Hai đường thẳng vuông góc:

Ta rất dễ dàng suy ra định nghĩa của hai đường thẳng vuông góc.

Định nghĩa. Hai đường thẳng vuông góc nếu góc giữa chúng là 90 độ. Kí hiệu: $a\bot b.$

Từ định nghĩa, ta có thể suy ra một số tính chất sau:

Tính chất.

Nếu $\overrightarrow{u},\overrightarrow{v}$ lần lượt là vector chỉ phương của hai đường thẳng a và b thì $\overrightarrow{u}.\overrightarrow{v}=0.$
Cho hai đường thẳng song song với nhau. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Hai đường thẳng vuông góc nhau thì có thể cắt nhau hoặc chéo nhau.

7. Đường thẳng vuông góc với mặt phẳng:

1. Định nghĩa:

Ta có định nghĩa sau về đường thẳng vuông góc với mặt phẳng:

$d\bot(P)\Leftrightarrow d\bot a,\forall a\subset (P).$

2. Điều kiện để đường thẳng vuông góc với mặt phẳng:

Để đường thẳng vuông góc với mặt phẳng, ta cần có điều kiện sau:

$\left\{\begin{matrix} a,b\subset (P),a\cap b=O\\d\bot a,d\bot b \end{matrix}\right.\Rightarrow d\bot (P).$

3. Tính chất:

Định nghĩa mặt phẳng trung trực: Mặt phẳng trung trực của một đoạn thẳng là mặt phẳng vuông góc với đoạn thẳng tại trung điểm của nó. (Mặt phẳng trung trực của đoạn thẳng là tập hợp các điểm cách đều hai đầu mút của đoạn thẳng đó).
$\left\{\begin{matrix} a//b\\(P)\bot a \end{matrix}\right.\Rightarrow (P) \bot b.$
$\left\{\begin{matrix} (P)//(Q)\\a\bot (P) \end{matrix}\right.\Rightarrow a\bot (Q).$
$\left\{\begin{matrix} a//(P)\\b\bot (P) \end{matrix}\right.\Rightarrow b\bot a.$
$\left\{\begin{matrix} a\neq b\\a\bot (P),b\bot (P) \end{matrix}\right.\Rightarrow a//b.$
$\left\{\begin{matrix} (P)\neq (Q)\\(P)\bot a,(Q)\bot a \end{matrix}\right.\Rightarrow (P)//(Q).$
$\left\{\begin{matrix} a\nsubseteq (P)\\a\bot b,(P)\bot b \end{matrix}\right.\Rightarrow a//(P).$

4. Định lí ba đường vuông góc:

Cho đường thẳng a không vuông góc với mặt phẳng (P), đường thẳng b thuộc mặt phẳng (P), a’ là hình chiếu của a lên (P). Khi đó:

$b\bot a\Leftrightarrow b\bot a'.$

5. Góc giữa đường thẳng và mặt phẳng:

Nếu d vuông góc với (P) thì góc giữa đường thẳng d và mặt phẳng (P) là 90 độ.
Nếu d không vuông góc với (P) thì $\widehat{(d,(P))}=\widehat{d,d'}$ với d’ là hình chiếu của d lên (P).
Chú ý: góc giữa đường thẳng và mặt phẳng là góc nhọn.

8. Hai mặt phẳng vuông góc:

1. Góc giữa hai mặt phẳng:

$\left\{\begin{matrix} a \bot(P)\\ b\bot(Q) \end{matrix}\right.\Rightarrow \widehat{((P),(Q))}=\widehat{(a,b)}.$
Chú ý: góc giữa (P) và (Q) là góc nhọn.

2. Diện tích hình chiếu của một đa giác:

Ta cần lưu ý công thức sau:

Gọi (S) là diện tích của đa giác (H) trong (P), S’ là diện tích của hình chiếu (H’) của (H) trên (Q), $\alpha =\widehat{((P),(Q))}.$

Khi đó:

$S'=S.cos\alpha .$

3. Hai mặt phẳng vuông góc:

Ta có định nghĩa và điều kiện sau của hai mặt phẳng vuông góc:

$(P)\bot(Q)\Rightarrow \widehat{((P),(Q))}=90^0.$
Điều kiện để hai mặt phẳng vuông góc với nhau: $\left\{\begin{matrix} (P)\supset a\\a\bot(Q) \end{matrix}\right.\Rightarrow (P)\bot(Q).$

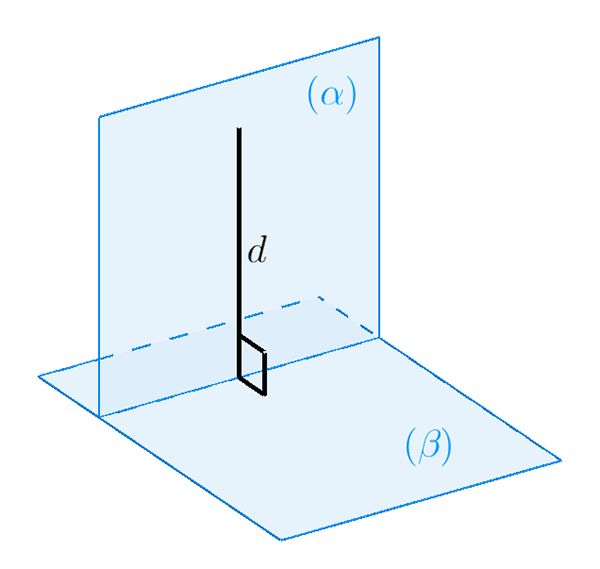
4. Tính chất của hai mặt phẳng vuông góc nhau:

Ta có các tính chất sau của hai mặt phẳng vuông góc nhau:

$\left\{\begin{matrix} (P)\bot(Q),(P)\cap (Q)=c\\a\subset (P),a\bot c \end{matrix}\right.\Rightarrow a\bot(Q).$
$\left\{\begin{matrix} (P)\bot(Q)\\A\in (P) \\a\ni A,a\bot(Q) \end{matrix}\right.\Rightarrow a\subset (P).$
$\left\{\begin{matrix} (P)\cap (Q)=a\\(P)\bot(R) \\(Q)\bot(R) \end{matrix}\right.\Rightarrow a\bot(R).$

9. Khoảng cách:

1. Khoảng cách từ một điểm tới một đường thẳng:

Cho điểm M và một đường thẳng $\Delta$ . Trong $mp(M,\Delta )$ gọi H là hình chiếu vuông góc của M trên $\Delta .$ Khi đó khoảng cách MH được gọi là khoảng cách từ điểm M đến $\Delta .$

2. Khoảng cách giữa hai đường thẳng:

Khoảng cách giữa hai đường thẳng $\Delta$ và $\Delta '$ .

Nếu hai đường thẳng đó cắt nhau hoặc trùng nhau thì góc giữa hai đường thẳng bằng 0 độ.
Nếu hai đường thẳng đó song song thì khoảng cách chính là hình chiếu của một điểm thuộc $\Delta$ đến đường thẳng $\Delta '.$

3. Khoảng cách từ một điểm đến một đường thẳng:

Cho mặt phẳng (P) và một điểm M, gọi H là hình chiếu của điểm M trên mặt phẳng (P). Khi đó MH được gọi là khoảng cách từ M đến (P).

Kí hiệu: d(M, (P)) = MH,

4. Khoảng cách từ một đường thẳng đến một mặt phẳng:

Cho đường thẳng y và mặt phẳng (P) song song với nhau. Khi đó khoảng cách từ một điểm bất kì trên y đến mặt phẳng (P) được gọi là khoảng cách giữa đường thẳng y và mặt phẳng (P).

5. Khoảng cách giữa hai mặt phẳng:

Cho hai mặt phẳng (P) và (Q) song song với nhau, khoảng cách từ một điểm bất kì trên mặt phẳng này đến mặt phẳng kia được gọi là khoảng cách giữa hai mặt phẳng (P) và (Q).

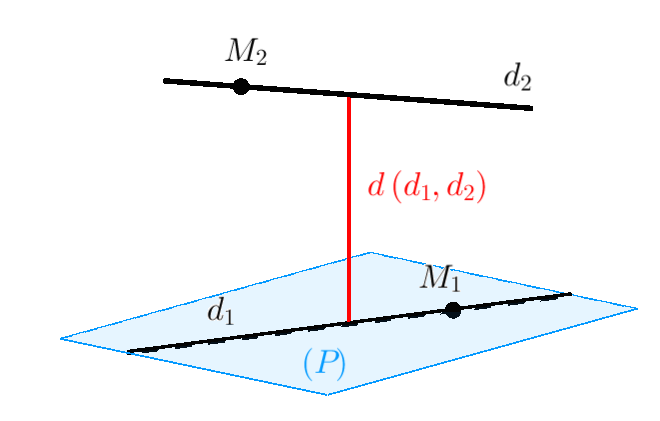
6. Khoảng cách giữa hai đường thẳng:

Cho hai đường thẳng chéo nhau a, b. Độ dài đoạn vuông góc chung MN của a và b được gọi là khoảng cách giữa hai đường thẳng a và b.

Nguyễn Nam Thành viên kể từ November 19, 2019

Người đóng góp