Bài 2: Dãy số

Định nghĩa

Một hàm số $\dpi{150} \textbf{u}$ xác định trên tập hợp các số nguyên dương $\mathbb{N}^*$ được gọi là một dãy số vô hạn (hay gọi tắt là dãy số).

$u_1 =u(1):$ số hạng thứ nhất (số hạng đầu)

$u_n =u(n):$ số hạng thứ n (số hạng tổng quát)

Chú ý:

Cho dãy số $u$ xác định trên tập hợp gồm $m$ số nguyên dương đầu tiên được gọi là một dãy số hữu hạn: $u_1, u_2, ..., u_m$ .

Khi này $u_{1}$ được gọi là số hạng đầu và $u_{m}$ được gọi là số hạng cuối.

Cách cho một dãy số

Cách 1: Cho dãy số với công thức của số hạng tổng quát

Ví dụ 1: Cho dãy $(u_n)$ với $u_n=\frac{2n-1}{n+1}$

Dãy số được viết dưới dạng khai triển là: $\frac{1}{2};1;\frac{5}{4}$

Cách 2: Cho dãy số bởi hệ thức truy hồi

Cho số hạng thứ nhất $u_1$ (hoặc một vài số hạng đầu)

Cho một công thức tính $u_n$ theo $u_{n-1}$ (hoặc một vài số hạng đầu)

Ví dụ 2: Cho dãy số $(u_n)$ xác định bởi $\left\{\begin{matrix} u_1=2\\ u_n=2u_{n-1}-1(n\geq2) \end{matrix}\right.$

Dạng khai triển của dãy số trên là: 2, 3, 5, 9, …

Cách 3: Diễn đạt bằng lời cách xác định của mỗi dãy số

Ví dụ 3: Cho hình vuông ABCD cạnh a. Cho dãy $(u_n)$ với $u_n$ là diện tích hình vuông có cạnh là $a^n$ .

Dãy số tăng, dãy số giảm

$(u_n)$ là dãy số tăng $\Leftrightarrow \forall n \in \mathbb{N^*},u_{n+1}>u_n$

$(u_n)$ là dãy số giảm $\Leftrightarrow \forall n \in \mathbb{N^*},u_{n+1}<u_n$

Phương pháp xét tính tăng giảm của dãy số

Cách 1: Xét dấu của hiệu số 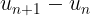$\large u_{n+1}-u_n$

Nếu $\forall n \in \mathbb{N^*},u_{n+1}-u_n>0$ thì $(u_n)$ là dãy số tăng.

Nếu $\forall n \in \mathbb{N^*},u_{n+1}-u_n<0$ thì $(u_n)$ là dãy số giảm.

Cách 2: Nếu 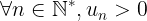$\large \forall n \in \mathbb{N^*},u_n>0$ thì có thể so sánh tỉ số 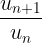$\large \frac{u_{n+1}}{u_n}$ với 1

Nếu $\frac{u_{n+1}}{u_n}>1$ thì $(u_n)$ là dãy số tăng.

Nếu $\frac{u_{n+1}}{u_n}<1$ thì $(u_n)$ là dãy số giảm.

Cách 3: Áp dụng phương pháp quy nạp

Nếu dãy số $(u_n)$ được cho bởi một hệ thức truy hồi thì thường dùng phương pháp chứng minh quy nạp để chứng minh $u_{n+1}>u_n$ (hoặc $u_{n+1}<u_n$ ), $\forall n\ \in\mathbb{N^*}$

Ví dụ 4: Xét tính tăng, giảm của dãy số $(u_n)=\frac{2n-1}{n+1}$

Bài giải

Ta có:

$\left\{\begin{matrix} u_n=2-\frac{3}{n+1}\\ u_{n+1}=2-\frac{3}{n+2} \end{matrix}\right.\\ \Rightarrow u_{n+1}-u_n=3\left (\frac{1}{n+1}-\frac{1}{n+2} \right )>0,\forall n \in \mathbb{N^*}$

Vậy $(u_n)$ là dãy số tăng

Dãy số bị chặn

Dãy bị chặn trên

Dãy số $(u_n)$ được gọi là dãy số bị chặn trên nếu tồn tại một số $M$ sao cho

$\LARGE \forall n \in \mathbb{N^*},u_n\leq M$

Dãy bị chặn dưới

Dãy số $(u_n)$ được gọi là dãy số bị chặn dưới nếu tồn tại một số $m$ sao cho

$\LARGE \forall n \in \mathbb{N^*},u_n\geq m$

Dãy bị chặn hai đầu

Dãy số $(u_n)$ được gọi là dãy số bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại một số $M$ và một số $m$ sao cho

$\LARGE \forall n \in \mathbb{N^*},m\leq u_n\leq M$

Ví dụ 5: Xét tính bị chặn của dãy số $(u_n)=\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{n.(n+1)}$

Bài giải

$(u_n)=\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{n.(n+1)}=1-\frac{1}{n+1}$

Ta có: $n\geq 1$

$\\\Rightarrow n+1\geq2\\ \\\Rightarrow \frac{-1}{n+1}\geq -\frac{1}{2}\\ \\\Rightarrow 1-\frac{1}{n+1}\geq \frac{1}{2}\\ \\\Rightarrow u_n\geq \frac{1}{2}, \forall n\in \mathbb{N^*}$