Bài 3: Nhị thức NEWTON

Công thức nhị thức Newton

\( (a + b) ^{n} = C_{n}^{0}.a^{n}.b^{0} + C_{n}^{1}.a^{n – 1}.b^{1} + … + C_{n}^{n}.a^{0}.b^{n} = \sum_{k = 0}^{n}(C^{k}_{n}.a^{n – k}.b^{k}) \)

Nhận xét:

Công thức nhị thức Newton (*) có:

• n+1 số hạng
• Số hạng tổng quát thứ k+1 là \( C^{k}_{n}.a^{n – k}.b^{k} \)
• Các hệ số có tính đối xứng: \( C^{k}_{n} = C^{n-k}_{n} \)
• Tổng số mũ cả a và b trong mỗi số hạng luôn bằng n

Ví dụ 1: Tìm số hạng có chứa \( x^{8} \) trong khai triển \((2x + 3)^{20}\)

Bài giải

Công thức số hạng tổng quát thứ k+1 là \( C^{k}_{20}.(2x)^{20- k}.3^{k} \)

Ta có: \( x^{8} = x^{20 – k} \Leftrightarrow k = 12 \)

Vậy số hạng có chứa x^8 là \( C^{12}_{20}.(2x)^{20 – 12}.3^{12} \)

Tam giác Pascal

Các hệ số của khai triển có thể xếp thành một tam giác gọi là tam giác Pascal.

? Có thể bạn chưa biết: TAM GIÁC PASCAL VÀ DÃY FIBONACY

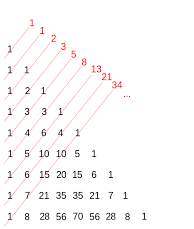
Chuyện gì sẽ xảy ra nếu chúng ta cộng các số hạng của tam giác Pascal theo đường chéo?

Khi cộng các số hạng của tam giác Pascal theo hướng đường chéo chính của nó, kết quả thu được là số Fibonacy, quả thật: