Định nghĩa
Cho
Hàm số dạng được gọi là hàm số mũ cơ số a.
Hàm số dạng được gọi là hàm số logarit cơ số a.
Lưu ý:
Kí hiệu dùng đề chỉ hàm số logarit cơ số 10.
Kí hiệu dùng để chỉ hàm số logarit cơ số e.
Một số giới hạn liên quan tới hàm số mũ và hàm số logarit
Người ta chứng minh được rằng:
Ví dụ 1: Tính các giới hạn sau:
a.
b.
Bài giải
a.
b.
Đạo hàm của hàm số mũ và hàm số logarit
Đạo hàm của hàm số mũ
Cho và K là một khoảng hay hợp của nhiều khoảng nào đó.
Hàm số có đạo hàm tại mọi điểm
và
Nói riêng:
Nếu là hàm số có đạo hàm trên K thì hàm số
có đạo hàm trên K và
Nói riêng:
Ví dụ 2: Tìm đạo hàm của hàm số
Bài giải
Đạo hàm của hàm số logarit
Cho và K là một khoảng hay hợp của nhiều khoảng nào đó
Hàm số có đạo hàm tại mọi điểm x>0 và
Nói riêng:
Nếu là hàm số nhận giá trị dương và có đạo hàm trên K thì hàm số
có đạo hàm trên K và:
Nói riêng:
Ví dụ 3: Chứng minh , ta có
Bài giải
, ta có:
Hệ quả
Nếu là hàm số nhận giá trị khác 0 và có đạo hàm trên K thì:
Sự biến thiên và đồ thị của hàm số mũ và hàm số logarit
Hàm số 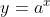
- Tập xác định:
- Đạo hàm:
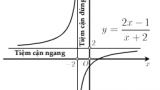
- Giới hạn và tiệm cận:
| TCN: y=0 ( |
||
| TCN: y=0 ( |
- Bảng biến thiên:
a>1


0<a<1


- Đồ thị hàm số luôn cắt trục tung tại điểm M(0;1) (do
) và nằm phía trên trục hoành


Hàm số 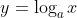
- Tập xác định:
- Đạo hàm:
- Giới hạn và tiệm cận:
| TCĐ: x=0 ( |
||
| TCĐ: x=0 ( |
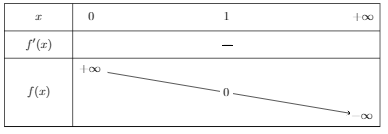
- Bảng biến thiên:
a>1


0<a<1


- Đồ thị hàm số luôn cắt trục tung tại điểm M(1;0) (do
) và nằm bên phải trục tung


Nhận xét: Đồ thị các hàm số và
đối xứng với nhau qua đường thằng
.


No Comments
Leave a comment Cancel