Bài 1: Lũy thừa số mũ hữu tỉ. Lũy thừa với số mũ thực.

Lũy thừa số mũ nguyên 

Định nghĩa

Lũy thừa số mũ nguyên dương

Cho , ta định nghĩa:

(n thừa số a)

là lũy thừa bậc n của a, a gọi là cơ số, n gọi là số mũ

Lũy thừa số mũ nguyên âm

Cho  , ta định nghĩa:

Chú ý:

và   không có nghĩa

 

Tính chất

Định lí 1

Cho . Khi đó ta có:

• 
• 
• 
• 
• 

Định lí 2

Cho . Khi đó, ta có:

Với :   (hàm số đồng biến)

Với :   (hàm số nghịch biến)

Hệ quả 1

Với và , ta có:

Hệ quả 2:

Với n là số tự nhiên lẻ, ta có:

 

Căn bậc n

Định nghĩa

Cho  là căn bậc n của a khi và chỉ khi:

Nhận xét:

     Với mỗi và n lẻ, có duy nhất một căn bậc n của a, kí hiệu .

     Với mỗi và n chẵn, có đúng hai căn bậc n của a, kí hiệu và , trong đó  và .

Tính chất

Cho , ta có:

• 
• 
• 
• 
• Nếu  thì

Lũy thừa với số mũ hữu tỉ

Định nghĩa

Cho a là một số thực dương, r là một số hữu tỉ có dạng , trong đó .

Ta định nghĩa:

Tính chất

Tương tự như của lũy thừa với số mũ nguyên được nêu ra ở trên.

 

Lũy thừa với số mũ vô tỉ

Định nghĩa

Cho a>0 và là một số vô tỉ.

Người ta chứng minh được rằng  luôn có một dãy số hữu tỉ  mà 

Xét những dãy số lũy thừa tương ứng:

Người ta chứng minh rằng dãy số  có giới hạn xác định chỉ phụ thuộc vào và  (không phụ thuộc vào dãy hữu tỉ đã chọn) khi .

Giới hạn đó được gọi là lũy thừa của với số mũ vô tỉ của số dương a. Kí hiệu là  .

Vậy:

trong đó  và

Ví dụ:

là giới hạn của dãy sau:

Nên là giới hạn của dãy sau:

 

Một số lưu ý về cơ số của lũy thừa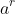

thì

thì (do và  vô nghĩa)

thì (do có )

Tính chất

Tương tự như của lũy thừa với số mũ nguyên được nêu ra ở trên.

 

Bài tập

1. Cho biểu thức , với . Xác định k để 
2. Cho , rút gọn biểu thức ?
3. Cho . Tính giá trị biểu thức 
4. Tính giá trị biểu thức 
5. Cho . Tính