Chương 2 chúng ta chủ yếu học về đường thẳng và mặt phẳng trong không gian, đồng thời là quan hệ song song trong không gian. Chương này có vai trò cực kì quan trọng trong thi học kì 1 và toàn bộ hình học không gian sau này.

A. Tóm tắt lí thuyết:

1. Đại cương về đường thẳng và mặt phẳng:

a. Tính chất cơ bản của hình học không gian

Ta thừa nhận các tính chất sau trong hình học không gian:

Tính chất.

– Tính chất duy nhất: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

– Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

– Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.

– Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

– Trong mỗi mặt phẳng, các kết quả đã biết (đã học) của hình học phẳng đều đúng.

Ta có định lí sau:

Định lí. Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.

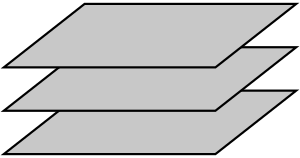
b. Điều kiện xác định mặt phẳng:

Ta xác định mặt phẳng nếu biết một trong những điều kiện sau:

Mặt phẳng đi qua ba điểm không thẳng hàng A, B, C. Ta kí hiệu là mp(ABC).
Mặt phẳng đi qua một đường thẳng a và một điểm A không thuộc đường thẳng a. Kí hiệu là mp(A, a).
Mặt phẳng đi qua hai đường thẳng cắt nhau a và b. Ta kí hiệu là mp(a, b).

c. Một số hình đặc biệt:

Ta lưu ý một số hình đặc biệt sau:

Tứ diện. Cho bốn điểm không đồng phẳng A, B, C, D. Hình tạo bởi bốn tam giác ABC, ACD, ADB, BCD được gọi là hình tứ diện.

Ta kí hiệu là tứ diện ABCD.

Tứ diện đều là tứ diện có bốn mặt là bốn tam giác đều.

Thiết diện (hay mặt cắt) của hình (H) khi cắt bởi mặt phẳng (P) là phần chung của mặt phẳng (P) và hình (H).

Trên đây là hình mô phỏng thiết diện.

2. Hai đường thẳng song song:

Ta có một số lưu ý sau về vị trí tương đối giữa hai đường thẳng phân biệt:

Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong mặt phẳng.
Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng.
Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung.

Image result for vị trí tương đối giữa hai đường thẳng phân biệt

Ta có một số tính chất về đường thẳng song song như sau:

Tính chất:

Trong không gian, qua một điểm năm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.
Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

Ngoài ra, ta có định lí về giao tuyến của ba mặt phẳng:

Định lí. Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy đồng qui hoặc đôi một song song.

Từ định lí này, ta suy ra được hệ quả sau:

Hệ quả. Nếu hai mặt phẳng cắt nhau lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng song song với hai đường thẳng đó (hoặc trùng với một trong hai đường thẳng đó).

3. Đường thẳng song song với mặt phẳng.

Ta có các định lí, định nghĩa và hệ quả cần nhớ sau:

Định nghĩa. Một đường thẳng và một mặt phẳng gọi là song song với nhau nếu chúng không có điểm chung.

Định lí 1. Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nào đó nằm trong (P) thì a song song với (P).

Định lí 2. Nếu đường thẳng a song song với mặt phẳng (P) thì mọi mặt phẳng (Q) chưa a mà cắt (P) thì cắt theo giao tuyến song song với a.

Hệ quả 1. Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó thuộc mặt phẳng.

Hệ quả 2. Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Định lí 3. Nếu a và b là hai đường thẳng chéo nhau thì qua a có một và chỉ một mặt phẳng song song với b.

4. Hai mặt phẳng song song.

a. Vị trí tương đối của hai mặt phẳng phân biệt:

Khi cho hai mặt phẳng phân biệt, thông thường sẽ có hai trường hợp xảy ra:

(P) và (Q) có điểm chung. Khi đó ta biết (P) và (Q) cắt nhau theo một đường thẳng.
(P) và (Q) không có điểm chung. Khi đó ta nói chúng song song với nhau, kí hiệu (P) // (Q).

Vậy từ đó, ta suy ra định nghĩa sau:

Định nghĩa. Hai mặt phẳng gọi là song song nếu chúng không có điểm chung.

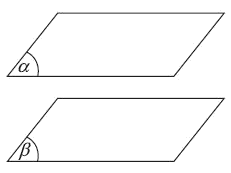
b. Điều kiện để hai mặt phẳng song song.

Ta có định lí sau:

Định lí. Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q) thì (P) song song với (Q).

Để chứng minh định lí trên, hãy giả sử (P) cắt (Q) tại c và suy ra điều vô lí.

c. Tính chất của hai mặt phẳng song song.

Từ định lí về hai mặt phẳng song song, ta có những tính chất sau đây:

Tính chất 1. Qua một điểm nằm ngoài một mặt phẳng, có một và chỉ một mặt phẳng song song với mặt phẳng đó (ta thấy khá giống với tiên đề Euclide trong đường thẳng).

Từ đây, ta có thể suy ra các hệ quả sau:

Hệ quả 1. Nếu đường thẳng a song song với mặt phẳng (Q) thì có duy nhất một mặt phẳng (P) chứa a và song song với (Q).

Hệ quả 2. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.

Ta đồng thời cũng có thêm một tính chất về hai mặt phẳng song song:

Tính chất 2.

Nếu hai mặt phẳng (P) và (Q) song song thì mọi mặt phẳng (R) đã cắt (P) thì phải cắt (Q) và các giao tuyến của chúng song song.