Tính đơn điệu của hàm số

Lí thuyết:

Định nghĩa:

Giả sử K là một khoảng (một đoạn, một nửa khoảng) và f là một hàm số xác định trên K. Khi đó:

Hàm số f đồng biến (đơn điệu tăng) trên K nếu và chỉ nếu $ \forall x_1,x_2\in K,x_1<x_2 $ thì $ f(x_1)<f(x_2). $
Hàm số f nghịch biến (đơn điệu giảm) trên K nếu và chỉ nếu $ \forall x_1,x_2\in K,x_1<x_2 $thì $ f(x_1)>f(x_2). $

Định lý

Định lí 1 – Điều kiện cần. Giả sử f là một hàm số có đạo hàm trên K.

Nếu hàm số f đồng biến trên K thì $ f'(x)>0 $ với mọi x thuộc K.
Nếu hàm số f nghịch biến trên K thì $ f'(x)<0 $ với mọi x thuộc K.

Định lí 2 – Điều kiện đủ. Giả sử hàm số f có đạo hàm tên K.

Nếu $ f'(x)>0,\forall x\in K$ thì hàm số f đồng biến trên K.
Nếu $ f'(x)<0,\forall x\in K$ thì hàm số f nghịch biến trên K.
Nếu $ f'(x)=0,\forall x\in K$ thì hàm số f không đổi trên K.

Định lí 3. Giả sử f(x) có đạo hàm trên K và phương trình f'(x) = 0 có hữu hạn nghiệm. Khi đó:

f(x) đồng biến trên K $ \Leftrightarrow f'(x)\geq 0,\forall x\in K.$ $\Leftrightarrow f'(x)\geq 0,\forall x\in K.$
f(x) nghịch biến trên K $ \Leftrightarrow f'(x)\leq 0,\forall x\in K.$

Các dạng bài tập:

Dạng 1: Tìm khoảng đơn điệu của hàm số:

Bài 1. Xét tính đơn điệu của các hàm số sau:

(a) $ y=x^3-6x^2+9x+1.$

(b) $ y=-\frac{1}{4}x^4-x^3+\frac{1}{2}x^2+3x.$

Bài 2. Xét tính đơn điệu của các hàm số sau:

(a) $ y=\frac{x+1}{\sqrt{x^2-x+1}}. $

(b) $ y=\frac{x^2}{\sqrt{x^2-1}}. $

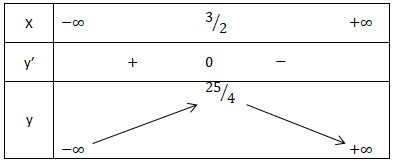
Ví dụ 1. Xét sự đồng biến, nghịch biến của hàm số $4+3x-x^2$

Tập xác định: D = R.

Ta có y’ = 3 – 2x suy ra y’= 0 tương đương với x = 3/2.

Khi x = 3/2 thì y = 25/4. Vậy ta có bảng biến thiên sau:

Dạng 2: Tìm điều kiện để hàm số đơn điệu trên một khoảng.

Bài 1. Tìm m để hàm số:

(a) $ y=\frac{1}{3}x^3+mx^2+(4m-3)x+3 $ đồng biến trên R.

(b) $ y=x^3-2mx+5 $ nghịch biến trên (- 2, 2).

Bài 2. Tìm m để hàm số:

(a) $ y=\frac{mx-m^2-1}{x+2} $ luôn tăng trên từng khoảng xác định.

(b) $ y=\frac{mx-3}{x-m+1} $ đồng biến trên (1; 2).

Ví dụ 2. Cho hàm số y = $f(x)=x^3-3mx+3(2m-1)x+1.$ Xác định m để hàm số đồng biến trên tập xác định.

f'(x) = $2x^2-6mx+3(2m-1)$

Để hàm số đồng biến suy ra $\Delta \leq 0, a> 0$ , giải ra m = 1.

Vậy m = 1 thì hàm số đồng biến trên R.

Dạng 3. Một số bài tập trắc nghiệm.

Bài 1. Hàm số $ y=\left | x^2-4x-5 \right | $ nghịch biến trên khoảng nào?

A. (-5; -1).

B. (-1; 2); (5; $ +\infty $).

C. (2; 5).

D. $ (-\infty;-1);(2;5). $ $(-\infty;-1);(2;5).$

Bài 2. Hàm số nào sau đây đồng biến trên R?

A. $ y=(x^2-1)^2-3x+2. $

B. $ y=\frac{x}{\sqrt{x^2+1}}. $

C. $ y=\frac{x}{x+1}. $

D. y = tanx.

Bài 3. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = (2m + 3)sinx + (2 – m)x đồng biến trên R?

A. 4.

B. 3.

C. 5.

D. 6.

Bài 4. Tìm m để phương trình $ x^2-2x+2m-3=0 $ có nghiệm thuộc [0; 9].

A. m < 2.

B. 1 < m < 2.

C. $ m\geq -30. $

D. $ -30\leq m\leq 2. $

Bài 5. Cho hàm số $ y=\frac{x^2-4x+m+2+3\sqrt{x^2-4x}}{\sqrt{x^2-4x}+2}. $ Có bao nhiêu giá trị nguyên dương của m để hàm số nghịch biến trên khoảng (- 4; – 1)?

A. 17.

B. 18.

C. 58.

D. 57.

lớp-12