1. Lí thuyết

1. Các đường tiệm cận:

Định nghĩa 1. Đường thẳng được gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu:

hoặc

Định nghĩa 2. Đường thẳng được gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu có ít nhất một trong các điều kiện sau được thỏa:

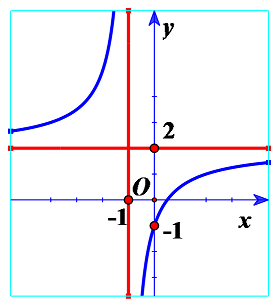
2. Các dạng toán cơ bản của đường tiệm cận:

1. Dạng 1. Tìm các đường tiệm cận của đồ thị hàm số:

Ví dụ 1. Tìm các đường tiệm cận đứng, tiệm cận ngang của các hàm số sau:

(a)

(b)

2. Dạng 2. Bài toán có chứa tham số:

Ví dụ 2. Tìm m để hàm số sau có 2 tiệm cận đứng

3. Bài tập trắc nghiệm:

1. Cho hàm số Khẳng định nào sau đây là đúng?

A. Đồ thị hàm số có tiệm cận đứng x = – 2.

B. Đồ thị hàm số có tiệm cận ngang y = – 1.

C. Đồ thị hàm số có tiệm cận đứng x = 2.

D. Đồ thị hàm số có tiệm cận ngang y = 2.

2. Tìm tiệm cận ngang của đồ thị hàm số

A. x = – 1.

B. y = – 1.

C. x = 2.

D. y = 2.

3. Đồ thị của hàm số có bao nhiêu tiệm cận đứng?

A. 2.

B. 1.

C. 3.

D. 4.

4. Đồ thị của hàm số nào sau đấy có tổng số đường tiệm cận đứng và ngang bằng 3?

A.

B.

C.

D.

5. Tìm số đường tiệm cận của đồ thị hàm số

A. 1.

B. 2. 

C. 3.

D. 0.

6. Cho hàm số Tìm số đường tiệm cận của đồ thị hàm số.

A. 0.

B. 1.

C. 2.

D. 3.

7. Cho hàm số Tìm số đường tiệm cận của đồ thị hàm số.

A. 0.

B. 1.

C. 2.

D. 3.

8. Cho đồ thị hàm số Đồ thị hàm số có đường tiệm cận nào?

A. Có tiệm cận đứng và tiệm cận ngang.

B. Chỉ có tiệm cận đứng.

C. Chỉ có tiệm cận ngang.

D. Không có tiệm cận.