Ôn tập chương 2

Câu hỏi

Các giá trị lượng giác của một góc α

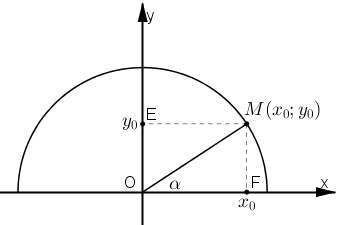
a. Trên nửa đường tròn lượng giác nằm phía trên trục hoành, xác định điểm M (x₀; y₀) sao cho $\widehat{MOx} =a$ . Khi đó ta có:

$sin a=y_{0}$
$cos a = x_{0}$
$tan a=\frac{y_{0}}{x_{0}}$
$cota=\frac{x_{0}}{y_{0}}$

b. Gọi E, F là hình chiếu của M trên Oy, Ox. Khi $a<90^{o}$ :

- $x_{0}>0, y_{0}>0$

- $sin a = y_{0} = \frac{MF}{OM}$

- $cos a=x_{0}=\frac{OF}{OM}$

Mối liên hệ giữa sin (cosin) của hai góc bù nhau

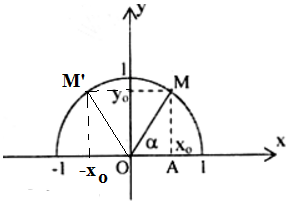
Gọi M (x_o; y_o) nằm trên nửa đường tròn đơn vị sao cho $\widehat{MOx} = a$

Khi đó điểm M’ (-x_o; y_o) trên nửa đường tròn đơn vị sao cho $\widehat{xOM'} = 180^{o} -a$

Ta có:

- $sina=y_{0} = sin(180^{o} -a)$
- $cosa = x_{0} = -(-x_{0}) = -cos(180^{o}-a)$

Tích vô hướng của hai vecto và tính chất

Tích vô hướng của hai vecto $\vec{a}$ và $\vec{b }$ :

$\vec{a}.\vec{b}=\left | \vec{a} \right |.\left | \vec{b} \right |.cos\left ( \vec{a};\vec{b} \right )$

Vì $-1\leq cos\left ( \vec{a} \right;\vec{b} )\leq 1$ nên ta có:

$-\left | \vec{a} \right |.\left | \vec{b} \right |\leq \vec{a}.\vec{b}\leq\left | \vec{a} \right |.\left | \vec{b} \right |$

$\vec{a}.\vec{b}$ đạt giá trị lớn nhất là $\left | \vec{a} \right |.\left | \vec{b} \right |$ khi $cos\left (\vec{a};\vec{b} \right )=1\Leftrightarrow \left (\vec{a};\vec{b} \right )=0$ ⇔ $\vec{a}$ và $\vec{b }$ cùng hướng.
$\vec{a}.\vec{b}$ đạt giá trị nhỏ nhất là $-\left | \vec{a} \right |.\left | \vec{b} \right |$ khi $cos\left (\vec{a};\vec{b} \right )=-1\Leftrightarrow \left (\vec{a};\vec{b} \right )=180^0$ ⇔ $\vec{a}$ và $\vec{b }$ ngược hướng.

Định lý Cosin trong tam giác

Tam giác ABC có AB = c, BC = a, AB = c thì ta có :

$cosA=\frac{b^2+c^2-a^2}{2bc}$

$cosB=\frac{a^2+c^2-b^2}{2ac}$

$cosC=\frac{a^2+b^2-c^2}{2ab}$

Định lý Sin và hệ quả

Trong tam giác ABC ta luôn có:

$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$ (Định lý Sin)

$\Rightarrow \left\{\begin{matrix} a=2R.sinA\\ b=2R.sinB\\ c=2R.sinC \end{matrix}\right.$

Quan hệ của a² và b² + c² khi góc A thay đổi?

Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :

$cosA=\frac{b^{2}+c^{2}-a^{2}}{2bc}$

Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b² + c² – a².

Góc A nhọn ⇔ cos A > 0 ⇔ b² + c² – a² > 0 ⇔ a² < b² + c².
Góc A tù ⇔ cos A < 0 ⇔ b² + c² – a² < 0 ⇔ a² > b² + c².
Góc A vuông ⇔ cos A = 0 ⇔ b² + c² – a² = 0 ⇔ a² = b² + c².

Bài tập áp dụng

Bài tập 1

Đề bài: Trong mặt phẳng Oxy cho vecto $\vec{a}=(-3;1)$ và vecto $\vec{b}=(2;2)$ . Hãy tính tích vô hướng $\vec{a}.\vec{b}$ .

Giải

Ta có:

$\vec{a}.\vec{b}=a_{1}.b_1+a_2.b_2$

Nên:

$\overrightarrow{a}.\overrightarrow{b}=(-3).2+(1.2)=-4$

Bài tập 2

Đề bài: Cho tam giác ABC có $\widehat{A}=60^0$ , BC = 6. Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Giải

Áp dụng định lý Sin trong tam giác ABC ta có:

$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$

Mà:

$\widehat{A}=60^0,a=BC=6.$

Do đó:

$2R=\frac{6}{sin60^0}$

$\Rightarrow R=\frac{6}{2sin60^0}=\frac{6}{\sqrt{3}}=2\sqrt{3}$

Vậy bán kính đường tròn ngoại tiếp tam giác bằng 2√3.

Bài tập 3

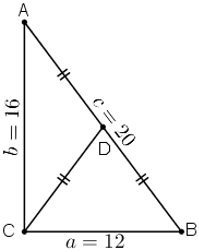
Đề bài: Cho tam giác ABC có a = 12, b = 16 và c = 20.Tính diện tích S tam giác, chiều cao h_a, các bán kính R, r của các đường tròn ngoại tiếp, nội tiếp tam giác và đường trung tuyến m_a của tam giác.

Giải

Diện tích tam giác: S = $\frac{1}{2}$ .a.b = $\frac{1}{2}$ .12.16 = 96 (đvdt)
Chiều cao h_a: h_a = AC = b = 16.
Tâm đường tròn ngoại tiếp tam giác là trung điểm của AB.
Bán kính đường tròn ngoại tiếp R = $\frac{AB}{2}=\frac{c}{2}$ = 10.
Bán kính đường tròn nội tiếp tam giác: S = p.r ⇒ r = $\frac{S}{p}$ trong đó S = 96 và p = $\frac{a+b+c}{2}$ = 24 ⇒ r = 4.