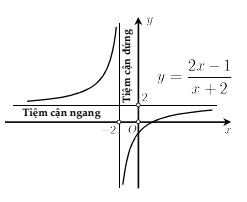
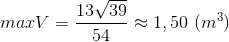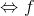Giải tích
Bài viết mới
Bài viết được yêu thích
Written by ღᏠᎮღmanhvipaceঔ
Written by ღᏠᎮღmanhvipaceঔ
Written by ღᏠᎮღmanhvipaceঔ
Written by ღᏠᎮღmanhvipaceঔ
Written by ღᏠᎮღmanhvipaceঔ
Written by ღᏠᎮღmanhvipaceঔ
Written by ღᏠᎮღmanhvipaceঔ
Written by ღᏠᎮღmanhvipaceঔ
Written by ღᏠᎮღmanhvipaceঔ
Written by ღᏠᎮღmanhvipaceঔ
Written by Phan Trần Minh Đạt
Written by sexspeakorg
Written by thuyvy848989